处理长序列
处理长序列
在长序列上训练一个RNN,必须运行很多时间步长,从而展开的RNN成为一个非常深的网络。就像任何深度神经网络一样,它可能会遇到不稳定的梯度问题:它可能永远在训练,或者训练可能会不稳定。此外,当RNN处理一个长序列时,它会逐渐忘记序列中的第一个输入。
应对不稳定梯度问题
在深度网络中用于应对不稳定梯度问题的许多技巧也可以用于RNN:良好的参数初始化、更快的优化器、dropout,等等。但是,非饱和激活函数(例如ReLU)在这里可能没有太大的帮助。实际上,它可能导致RNN在训练过程中变得更加不稳定。假设梯度下降以一种在第一个时间步长稍微增加输出的方式来更新权重。由于每个时间步长都使用相同的权重,因此第二个时间步长的输出也可能会略有增加,第三个时间步长的输出也会稍有增加,以此类推,直到输出爆炸为止,而非饱和激活函数不能阻止这种情况。可以使用较小的学习率来降低这种风险,但也可以使用饱和激活函数(例如双曲正切)(这解释了为什么将其设定为默认值)。同样的方式,梯度本身也会爆炸。
此外,批量归一化不能像深度前馈网络那样高效地用于RNN。实际上,不能在时间步长之间使用它,而只能在递归层之间使用,更准确地说,从技术上讲,可以在记忆单元中添加一个BN层,以便将其应用于每个时间步长(在该时间步长和前一个时间步长的隐藏状态上)。但是,在每个时间步长都是用相同的BN层,并使用相同的参数,而不管输入的实际比例和偏移以及隐藏状态如何。在实践中,这不能产生良好的效果,BN仅在将BN应用于输入而非隐藏状态时才稍微收益。当应用于循环层之间时,它总比没有好,但不是在递归层中。在Keras中,可以简单地在每个递归层之前添加一个BatchNormalization层来完成此操作
归一化的另一种形式通常与RNN一起使用会更好:层归一化:它和批量归一化非常相似,但是它不是跨批量维度进行归一化,而是在特征维度上进行归一化。它的一个优点是可以在每个时间步长上针对每个实例独立地即时计算所需的统计信息。这也意味着它在训练和测试期间的行为方式相同(与BN相反),并且不需要使用指数移动平均值来估计样本中所有实例的特征统计信息。像BN一样,层归一化学习每个输入的比例和偏移参数。在RNN中,通常在输入和隐藏状态的线性组合后立即使用它
使用tf.keras在一个简单的记忆单元中实现层归一化。为此需要自定义个自定义记忆单元。就像常规层一样,不同处在于其call()方法采用两个参数:当前时间步长的inputs和上一个时间步长的隐藏states。states参数是包含一个或多个张量的列表。对于简单的RNN单元,它包含的单个张量等于上一个时间步长的输出,但是其他单元可能具有多个状态张量(例如,LSTMCell具有长期状态和短期状态)。一个单元必须具有state_size属性和output_size属性。在简单的RNN中,两者都等于单元数量。以下代码实现了一个简单的记忆单元,该单元的行为类似于SimpleRNNCell,不同之处在于它还在每个时间步长应用“层归一化”
import tensorflow as tf
from tensorflow import keras
class LNSimpleRNNCell(keras.layers.Layer):
def __init__(self, units, activation='tanh', **kwargs):
super().__init__(**kwargs)
self.state_size = units
self.output_size = units
self.simple_rnn_cell = keras.layers.SimpleRNNCell(units, activation=None)
self.layer_norm = keras.layers.LayerNormalization()
self.activation = keras.activation.get(activation)
def call(self, inputs, states):
outputs, new_states = self.simple_rnn_cell(inputs, states)
norm_outputs = self.activation(self.layer_norm(outputs))
return norm_outputs, [norm_outputs]LNSimpleRNNCell类继承自keras.layers.Layer类,就像任何自定义层一样。构造函数采用单元数量和所需激活函数,并设置state_size和output_size属性,然后创建一个没有激活函数的SimpleRNNCell(因为要在线性运算之后但在激活函数之前执行“层归一化”),然后,构造函数创建LayerNormalization层,最后获取需要的激活函数。call()函数通过应用于简单的RNN单元开始,该单元计算当前输入和先前输出的隐藏状态的线性组合,并返回两个结果(实际上,在SimpleRNNCell中,输出等于隐藏状态:也就是new_states[0]=outputs,因此可以在其他的call()方法中安全的忽略new_states)。接下来call()方法应用“层归一化”,然后跟随一个激活函数。最后,它返回两个输出(一个作为输出,另一个作为新的隐藏状态)。要使用此自定义单元,需要做的就是创建一个keras.layers.RNN层,并向其传递一个单元实例:
model = keras.models.Sequential([
keras.layers.RNN(LNSimpleRNNCell(20), return_sequences=True, input_shape=[None, 1]),
keras.layers.RNN(LNSimpleRNNCell(20), return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])同样可以创建一个自定义单元在每个时间步长之间应用dropout。但是有一种更简单的方法:所有循环层(除kears.layers.RNN之外)和Keras提供的所有单元都有一个超参数dropout和一个超参数recurrent_dropout:前者定义了应用于步长的dropout率(在每个时间步长),后者定义隐藏状态的dropout率(也在每个时间步长)。
在RNN中使用这些技术,可以缓解不稳定的梯度问题,更有效地训练RNN
解决短期记忆问题
由于数据在遍历RNN时会经过转换,因此在每个时间步长都会丢失一些信息。一段时间后,RNN的状态几乎没有任何最初输入的痕迹。这是一个热门问题,想象一下试图翻译一个长句子,当读完句子后,不知道如何开始。为了解决这个问题,引入了具有长期记忆的各种类型的单元。它们被证明非常成功,以至于不再使用基本的单元了
LSTM单元
长短期记忆(LSTM)单元由Sepp Hochriter和Jurgen Schmidhuber于1997年提出,并在随后的几年中由Alex Graves、Hasim Sak和Wojciech Zaremba等几位研究者逐步改进。如果把LSTM单元视作黑盒子,则它可以像基本单元一样使用,组它的性能会更好:训练会收敛得更快,它会检测数据中的长期依赖性。在Keras中,可以简单地使用LSTM层:
model = keras.models.Sequential([
keras.layers.LSTM(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.LSTM(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])或者,可以使用通用的keras.layers.RNN层,为其提供LSTMCell作为参数:
model = keras.models.Sequential([
keras.layers.RNN(keras.layers.LSTMCell(20), return_sequences=True, input_shape=[None, 1]),
keras.layers.RNN(keras.layers.LSTMCell(20), return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])LSTM层在GPU上运行时会使用优化过的实现,因此通常最好使用它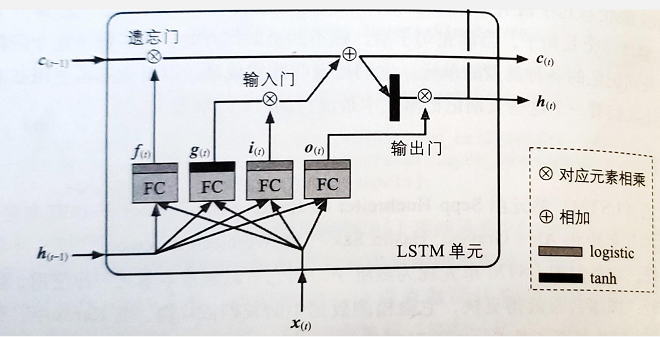
不过不查看框内的内容,则LSTM单元看起来与常规单元完全一样,除了它的状态被分为两个向量:$h_{(t)}$和$c_{(t)}$(‘c’代表“单元cell“。$h_{(t)}$视为短期状态,$c_{(t)}$为长期状态
LSTM单元关键的思想是网络可以学习长期状态下存储的内容、丢弃的内容以及从中读取的内容。当长期状态$c_{(t-1)}$从左到右遍历网络时,可以看到它首先经过了一个遗忘门,丢掉了一些记忆,然后通过加法操作添加了一些新的记忆(由输入门选择的记忆)。结果$c_{(t)}$直接送出来,无需任何进一步的转换。因此,在每个时间步长中,都会丢掉一些记忆,并添加一些记忆。此外,在加法运算之后,长期状态被复制并通过tanh函数传输,然后结果被输出门滤波。这将产生短期状态$h_{(t)}$(等于该时间步长的单元输出$y_{(t)}$)
首先,将当前输入向量$x_{(t)}$和先前的短期状态$h_{(t-1)}$馈入四个不同的全连接层。它们都有不同的目的:
- 主要层是输出$g_{(t)}$的层。它通常的作用是分析当前输入$x_{(t)}$和先前(短期)状态$h_{(t-1)}$。在基本单元中,除了这一层,没有其他的东西,它的输出直接到$y_{(t)}$和$h_{(t)}$。相比之下,在LSTM单元中,该层的输出并非直接输出,而是将其最重要的部分存储在长期状态中(其余部分则丢弃)
其他三层是门控制器。由于它们使用逻辑激活函数,因此它们的输出范围是0到1。它们的输出被馈送到逐元素乘法运算,因此如果输出0则关闭门,输出1则将门打开。特别地:
- 遗忘门(由$f_{(t)}$控制)控制长期状态的哪些部分应当被删除
- 遗忘门(由$i_{(t)}$控制)控制应将$g_{(t)}$的哪些部分添加到长期状态
- 最后,输出门(由$o_{(t)}$控制)控制应在此时间步长读取长期状态的哪些部分并输出到$h_{(t)}$和$y_{(t)}$
简而言之,LSTM单元可以学会识别重要的输入(这是输入门的作用),将其存储在长期状态中,只要需要就保留它(即遗忘门的作用),并在需要时将其提取出来。这就解释了为什么这些单元在识别时间序列、长文本、录音等长期模式方面取得了惊人的成功
下列公式总结了如果计算单个实例在每个时间步长的单元的长期状态、短期状态以及其输出(与整个小批量的方程非常类似):
$$ \begin{align*}i(t)=&\sigma(W_{xi}^Tx_{(t)}+W_{hi}^Th_{(t-1)}+b_i)\\ f_{(t)}=&\sigma(W_{xf}^Tx_{(t)}+W_{hf}h_{(t-1)}+b_f)\\ o_{(t)}=&\sigma(W_{xo}^T+W_{ho}^Th_{(t-1)}+b_o)\\ g_{(t)}=&tanh(W_{xg}^Tx_{(t)}+W_{hg}^Th_{(t-1)}+b_g)\\ c_{(t)}=&f_{(t)}\otimes c_{(t-1)}+i_{(t)}\otimes g_{(t)}\\ y_{(t)}=&h_{(t)}=o_{(t)}\otimes tanh(c_{(t)}\\ \end{align*} $$
在此等式中:
- $W_{xi},W_{xf},W_{xo},W_{xg}$是四层中每层与输入向量$x_{(t)}$连接的权重矩阵
- $W_{hi},W_{hf},W_{ho},W_{hg}$是四层中的每层与先前的短期状态$h_{(t-1)}$连接的权重矩阵
- $b_i,b_f,b_o,b_g$是四层中每层的偏置项。TensorFlow将$b_f$初始化为一个全是1不是0的向量。这样可以防止在训练开始时忘记一切
窥视孔连接
在常规LSTM单元中,门控制器只能查看输入$x_{(t)}$和先前的短期状态$h_{(t-1)}$。通过让它们也查看长期状态来给它们更多的功能,这可能是一个好主意。Felix Gers和Jergen Schmidhuber于2020年提出了这个想法。他们提出了一种带有额外连接的LSTM变体,称为窥视孔连接:先前的连接状态$c_{(t-1)}$作为输入添加到输出门的控制器。这通常会提高性能,但并非总是如此,并且没有明确的模式说明哪个任务更好。
在Keras中,LSTM层基于不支持窥视孔的keras.layers.LSTMCell单元。实验性的tf.keras.experimental.PeepholeLSTMCell可以,因此可以创建keras.layers.RNN层,并将PeepholeLSTMCell传递给其构造函数。LSTM单元还有许多其他变体。一种特别流行的变体是GRU单元
GRU单元
门控循环单元(Gated Recurrent Unit,GRU)是由Kyunghyun Cho等人在2014年的论文中提出的,该论文还介绍了Encoder-Decoder网络
GRU单元式LSTM单元的简化版,但它的性能也不错。以下是主要的简化:
- 两个状态向量合并为一个向量$h_{(t)}$
- 单个门控制器$z_{(t)}$控制遗忘门和输入门。如果门控制器输出1,则遗忘门打开,输入门关闭。如果输出0,则相反。无论何时记忆需要被存储,其存储位置需要首先被删除。实际上,这本身就是LSTM单元的常见变体
- 没有输出门,在每个时间步长都输出完整的状态向量。但是,有一个新的门控制器$r_{(t)}$控制先前状态的哪一部分将显示给主要层$g_{(t)}$
GRU计算公式
$$ \begin{align*}z_{(t)}=&\sigma(W_{xz}^Tx_{(t)}+W_{hz}^Th_{(t-1)}+b_z)\\ r_{(t)}=&\sigma(W_{xr}^Tx_{(t)}+W_{hr}^Th_{(t-1)}+b_r)\\ g_{(t)}=&tanh(W_{xg}^Tx_{(t)}+W_{hg}^T(r_{(t)}\otimes h_{(t-1)})+b_g)\\ h_{(t)}=&z_{(t)}\otimes h_{(t-1)}+(1-z_{(t)})\otimes g_{(t)} \end{align*} $$
Keras提供了一个keras.layers.GRU层(基于keras.layers.GRUCell记忆单元),使用它只是用GRU来替换SimpleRNN或LSTM的问题。
LSTM和GRU单元是RNN成功的主要原因之一。尽管它们可以处理比RNN更长的序列,但它们的短期记忆仍然非常有限,而且很难学习100个或更多时间步长时间序列的长期模式,例如音频样本、长时间序列或长句子。解决这个问题的一种方法是缩短输入序列,例如使用一位卷积层。
使用一维卷积层处理序列
2D卷积层的工作原理是在图像上滑动几个相当小的内核(或过滤器),生成多个2D特征图(每个内核一个)。类似地,一维卷积层在一个序列上滑动多个内核,为每个内核生成一维卷积图。每个内核将学习检测单个非常短的顺序模式(不长于内核大小)。如果使用10个内核,则该层的输出将由10个一维的序列(所有长度相同)组成,或者等效地,可以将此输出视为单个10维的序列。这意味着可以构建由循环层和一维卷积层(甚至一维池化层)混合而成的神经网络。如果使用步幅为1且填充为'same'的一维卷积层,则输出序列的长度和输入序列的长度相同。但是,如果使用1填充为’valid‘或步幅大于1,则输出序列比输入序列短,因此需要确保相应地调整目标。
例如,一下模型与前面模型相同,不同之处在于它从一维卷积层开始,将输入序列进行2倍下采样,使用步幅为2。内核大小大于步幅,因此所有的输入将被用来计算层的输出,因此该模型可以学习保留有用的信息,而只删除不重要的细节。通过缩短序列,卷积层可以帮助GRU检测更长的模式。需要注意的是,还必须裁剪掉目标中的前三个时间步长(因为内核大小为4,所有卷积层的第一个输出将基于0至3的输入是时间步长),并对目标进行2倍的下采样
import numpy as np
import tensorflow as tf
from tensorflow import keras
def generate_time_series(batch_size, n_steps):
freq1, freq2, offsets1, offsets2 = np.random.rand(
4, batch_size, 1) # 生成4个,(batch_size,1)形状的矩阵
time = np.linspace(0, 1, n_steps) # 时间为将0-1划分为n_steps个时间步长
series = .5*np.sin((time-offsets1)*(freq1*10+10)) # 创建时间序列数值:sin(时间-相位)*频率)
series += .2*np.sin((time-offsets2)*(freq2*20+20))
series += .1*(np.random.rand(batch_size, n_steps)-.5) # 添加噪声
return series[..., np.newaxis].astype(np.float32)
n_steps = 50
series = generate_time_series(10000, n_steps+10)
X_train, Y_train = series[:7000, :n_steps], series[:7000, -10:,0]
X_valid, Y_valid = series[7000:9000, :n_steps], series[7000:9000, -10:,0]
X_test, Y_test = series[9000:, :n_steps], series[9000:, -10:,0]
Y = np.empty((10000, n_steps, 10))
for step_ahead in range(1, 10+1):
Y[:, :, step_ahead-1] = series[:, step_ahead:step_ahead +
n_steps, 0] # 创建时间序列,将预测目标设置为X后n_steps个时间步的数据作为序列中的一个数据,时间步与X相同但是是一个拥有10个数值的序列
Y_train = Y[:7000]
Y_valid = Y[7000:9000]
Y_test = Y[9000:]
print(series.shape)
print(X_train.shape)
print(Y_train.shape)
def last_time_step_mse(Y_true, Y_pred):
return keras.metrics.mean_squared_error(Y_true[:, -1], Y_pred[:, -1])
model=keras.models.Sequential([
keras.layers.Conv1D(filters=20,kernel_size=4,strides=2,padding='valid',input_shape=[None,1]),
keras.layers.GRU(20,return_sequences=True),
keras.layers.GRU(20,return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
model.compile(loss='mse',optimizer='adam',metrics=[last_time_step_mse])
history=model.fit(X_train,y_train[:,3::2],epochs=20,
validtion_data=(X_valid,Y_valid[:,3::2]))(10000, 60, 1)
(7000, 50, 1)
(7000, 50, 10)
Epoch 1/20
219/219 [==============================] - 4s 11ms/step - loss: 0.0705 - last_time_step_mse: 0.0629 - val_loss: 0.0464 - val_last_time_step_mse: 0.0399
Epoch 2/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0403 - last_time_step_mse: 0.0328 - val_loss: 0.0358 - val_last_time_step_mse: 0.0284
Epoch 3/20
219/219 [==============================] - 2s 9ms/step - loss: 0.0312 - last_time_step_mse: 0.0215 - val_loss: 0.0282 - val_last_time_step_mse: 0.0176
Epoch 4/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0260 - last_time_step_mse: 0.0150 - val_loss: 0.0251 - val_last_time_step_mse: 0.0137
Epoch 5/20
219/219 [==============================] - 2s 9ms/step - loss: 0.0240 - last_time_step_mse: 0.0130 - val_loss: 0.0238 - val_last_time_step_mse: 0.0125
Epoch 6/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0231 - last_time_step_mse: 0.0123 - val_loss: 0.0231 - val_last_time_step_mse: 0.0122
Epoch 7/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0222 - last_time_step_mse: 0.0116 - val_loss: 0.0225 - val_last_time_step_mse: 0.0117
Epoch 8/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0218 - last_time_step_mse: 0.0113 - val_loss: 0.0218 - val_last_time_step_mse: 0.0109
Epoch 9/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0212 - last_time_step_mse: 0.0108 - val_loss: 0.0216 - val_last_time_step_mse: 0.0108
Epoch 10/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0207 - last_time_step_mse: 0.0103 - val_loss: 0.0209 - val_last_time_step_mse: 0.0101
Epoch 11/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0202 - last_time_step_mse: 0.0099 - val_loss: 0.0207 - val_last_time_step_mse: 0.0100
Epoch 12/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0198 - last_time_step_mse: 0.0095 - val_loss: 0.0200 - val_last_time_step_mse: 0.0093
Epoch 13/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0192 - last_time_step_mse: 0.0090 - val_loss: 0.0194 - val_last_time_step_mse: 0.0088
Epoch 14/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0185 - last_time_step_mse: 0.0083 - val_loss: 0.0187 - val_last_time_step_mse: 0.0079
Epoch 15/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0178 - last_time_step_mse: 0.0075 - val_loss: 0.0181 - val_last_time_step_mse: 0.0076
Epoch 16/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0170 - last_time_step_mse: 0.0066 - val_loss: 0.0173 - val_last_time_step_mse: 0.0064
Epoch 17/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0164 - last_time_step_mse: 0.0060 - val_loss: 0.0165 - val_last_time_step_mse: 0.0057
Epoch 18/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0159 - last_time_step_mse: 0.0054 - val_loss: 0.0162 - val_last_time_step_mse: 0.0055
Epoch 19/20
219/219 [==============================] - 2s 9ms/step - loss: 0.0154 - last_time_step_mse: 0.0050 - val_loss: 0.0157 - val_last_time_step_mse: 0.0049
Epoch 20/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0151 - last_time_step_mse: 0.0047 - val_loss: 0.0153 - val_last_time_step_mse: 0.0046
32/32 [==============================] - 0s 3ms/step - loss: 0.0149 - last_time_step_mse: 0.0044
[0.014898738823831081, 0.0043519060127437115]精度为0.004是目前为止最好的模型,卷积层确实有帮助。
WaveNet
在2016年的一篇论文中,介绍了一种称为WaveNet的架构。他们堆叠了一维卷积层,使每一层的扩散(dilation)率(每个神经元输入的分散程度)加倍:第一个卷积层一次只看到两个时间步长,而下一个卷积层一次看到四个时间步长(其接受视野为四个时间步长),下一次看到8个时间步长,以此类推。这样,较低的层学习短期模式,而较高的曾学习长期模式。由于扩散率的加倍,网络可以非常有效地处理非常大的序列。
在WaveNet论文中,作者实际上堆叠了10个卷积层,其扩散率为1、2、4、8,···,256,512,然后又堆叠了另一组10个相同的层(扩散率也分别为1、2、4、8,···,256,512),然后又是另一组相同的10层。它们通过指出具有这些扩散率的10个卷积层的单个堆栈1来证明该结构的合理性,就像内核大小为1024的超高效卷积层一样工作(除了更快、更强大且使用更少的参数之外),这就是为什么它们堆叠了3个这样的块。它们还对输入序列进行了左填充,这些零与每个层之前的扩散率相等,以保证整个网络中相同的序列长度,以下实现了简化的WaveNet来处理和之前相同的序列:
model=keras.models.Sequential()
model.add(keras.layers.InputLayer(input_shape=[None,1]))
for rate in (1,2,4,8)*2:
model.add(keras.layers.Conv1D(filters=20,kernel_size=2,padding='causal',activation='relu',dilation_rate=rate))
model.add(keras.layers.Conv1D(fliters=10,kernel_size=1))
model.compile(loss='mse',optimizer='adam',metrics=[last_time_step_mse],validation_data=(X_valid,Y_valid))
history=model.fit(X_train,Y_train,epochs=20,validation_data=(X_valid,Y_valid))
model.evaluate(X_test,Y_test)Epoch 1/20
219/219 [==============================] - 3s 9ms/step - loss: 0.0700 - last_time_step_mse: 0.0577 - val_loss: 0.0377 - val_last_time_step_mse: 0.0237
Epoch 2/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0318 - last_time_step_mse: 0.0185 - val_loss: 0.0299 - val_last_time_step_mse: 0.0170
Epoch 3/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0274 - last_time_step_mse: 0.0150 - val_loss: 0.0264 - val_last_time_step_mse: 0.0138
Epoch 4/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0258 - last_time_step_mse: 0.0137 - val_loss: 0.0255 - val_last_time_step_mse: 0.0133
Epoch 5/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0247 - last_time_step_mse: 0.0128 - val_loss: 0.0246 - val_last_time_step_mse: 0.0125
Epoch 6/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0239 - last_time_step_mse: 0.0121 - val_loss: 0.0236 - val_last_time_step_mse: 0.0116
Epoch 7/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0232 - last_time_step_mse: 0.0114 - val_loss: 0.0231 - val_last_time_step_mse: 0.0110
Epoch 8/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0227 - last_time_step_mse: 0.0110 - val_loss: 0.0225 - val_last_time_step_mse: 0.0106
Epoch 9/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0221 - last_time_step_mse: 0.0105 - val_loss: 0.0222 - val_last_time_step_mse: 0.0102
Epoch 10/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0216 - last_time_step_mse: 0.0099 - val_loss: 0.0217 - val_last_time_step_mse: 0.0097
Epoch 11/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0212 - last_time_step_mse: 0.0096 - val_loss: 0.0214 - val_last_time_step_mse: 0.0093
Epoch 12/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0207 - last_time_step_mse: 0.0089 - val_loss: 0.0211 - val_last_time_step_mse: 0.0087
Epoch 13/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0203 - last_time_step_mse: 0.0085 - val_loss: 0.0203 - val_last_time_step_mse: 0.0080
Epoch 14/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0198 - last_time_step_mse: 0.0079 - val_loss: 0.0213 - val_last_time_step_mse: 0.0092
Epoch 15/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0196 - last_time_step_mse: 0.0078 - val_loss: 0.0202 - val_last_time_step_mse: 0.0077
Epoch 16/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0193 - last_time_step_mse: 0.0075 - val_loss: 0.0199 - val_last_time_step_mse: 0.0077
Epoch 17/20
219/219 [==============================] - 2s 7ms/step - loss: 0.0190 - last_time_step_mse: 0.0073 - val_loss: 0.0200 - val_last_time_step_mse: 0.0076
Epoch 18/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0188 - last_time_step_mse: 0.0069 - val_loss: 0.0193 - val_last_time_step_mse: 0.0070
Epoch 19/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0187 - last_time_step_mse: 0.0069 - val_loss: 0.0195 - val_last_time_step_mse: 0.0073
Epoch 20/20
219/219 [==============================] - 2s 8ms/step - loss: 0.0183 - last_time_step_mse: 0.0067 - val_loss: 0.0188 - val_last_time_step_mse: 0.0066
32/32 [==============================] - 0s 8ms/step - loss: 0.0183 - last_time_step_mse: 0.0063
[0.018330231308937073, 0.006296257022768259]MSE到达了0.0063
该Sequential模型从显示输入层开始,然后继续使用填充为“causal”的一维卷积层:这确保卷积层在进行预测时不会窥视未来(它等效于在输入的左侧填充正确数量的零且使用’valid‘填充)。然后添加类似的成对层,使用不断扩大的扩散率:1、2、4、8,还是1、2、4、8.最后添加输出层:一个具有10个大小为1的滤波器且没有任何激活函数的卷积层。多亏了填充层,每个卷积层都输出和输入序列长度相同的序列,因此在训练过程中使用的目标是完整序列,无需将裁减或对它们进行下采样。
到目前为止,最后两个模型在预测时间序列方面提供了最佳性能。在WaveNet论文中,作者在各种音频任务(架构的名称)上获得了最先进的性能,包括从文本到语音的任务,在多种语言中产生了令人难以置信的逼真的声音。他们还是用该模型来生成音乐,一次生成一个音频样本。当意识到一秒钟的音频可以包含数万个时间步长时,这一成就会更加令人印象深刻,甚至LSTM和GRU都无法处理如此长的序列。